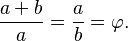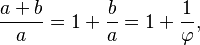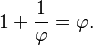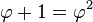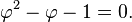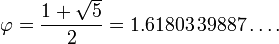PRAKATA

03.33 |

 Selamat Datang :)


 "Geometry has two great treasure : one is the Theorem of Phytagoras, the other is division of a line into extreme and mean ratio. The first we may compare to a measure of gold, the second we may name a precious jewel."

-Johannes Kepler


Dari kutipan diatas, Johannes Kepler menyatakan bahwa terdapat dua penemuan hebat dalam geometri yaitu Teorema Phitagoras dan Extreme and mean ratio atau yang biasa dikenal sebagai Golden Ratio.

Dalam blog ini, kami  yang beranggotakan :

  1. Muhammad Ardiyansyah
  2. Ariffah Nur Himawati
  3. Diana Vitelanoka Purwandani
  4. Salsabella Tristya Putri
  5. Dian Untari
  6. Chairatin Nisa

akan membahas mengenai salah satu dari penemuan terbesar dalam geometri tersebut yaitu Golden Ratio.


Golden Ratio merupakan istilah matematika untuk kondisi dimana jumlah kedua angka dibagi angka A sama dengan angka A dibagi angka B, dimana A > B.

( sumber )
Golden Ratio banyak digunakan dalam berbagai bidang tidak hanya geometri. Dan Golden Ratio juga sering dilambangkan sebagai angka keindahan. Dari sini maka kita dapat menarik kesimpulan bahwa matematika bukan hanya sebuah perhitungan belaka, di matematika kita belajar keindahan secara tersirat ataupun tersurat.

Di sini kami hanya menjelaskan salah satu dari sekian banyak bagian matematika yang menyimbolkan keindahan. Dan Golden Ratio hanyalah salah satu konsep pendekatan untuk menjelaskan proporsi ideal untuk menciptakan keindahan. Karena ini merupakan salah satu dari sekian banyak konsep, kita tidak perlu terpaku dengan hanya menggunakan golden ratio. Namun dengan memahami konsep golden ratio, kita memiliki salah satu metode untuk mempermudah menilai keindahan dengan metode yang kuantitatif. (sumber)

Sekian prakata dari kami. Selamat menggunakan golden ratio. Semoga blog ini dapat menambah pengetahuan Anda. Terimakasih :)





  • Digg
  • Del.icio.us
  • StumbleUpon
  • Reddit
  • RSS
Read User's Comments0
Diposting oleh the beautiful proportion

Sejarah Golden Ratio

04.04 |

Diawali oleh Phidias, pematung terkemuka asal Yunani pada abad sebelum masehi kemudian Golden Ratio terus berkembang. Masih pada abad sebelum masehi, Golden Ratio ditemukan dalam karya Plato yang kemudian pada abad selanjutnya Golden Ratio didefinisikan oleh Euclid.



http://biography.edigg.com/Phidias.shtml

    Phidias (Φειδίας; circa 480 SM – 430 SM) adalah seorang pematung, pelukis dan arsitek Yunani Kuno. Dia hidup pada abad ke- 5 SM dan disebut-sebut sebagai pematung terhebat pada masa Yunani Klasik. Patung Zeus karya Phidias merupakan salah satu dari Tujuh Keajaiban Dunia Kuno. Phidias juga merancang patung dewi Athena di Akropolis Athena yang dinamai Athena Parthenos di dalam bangunan  Parthenon dan juga patung Athena Promachos, patung perunggu dewi Athena yang kolosal yang berdiri di antara Athena Parthenos Propilaila, pintu gerbang monumental yang berfungsi sebagai jalan masuk Akropoilis. Phidias adalah putra Kharmides dari Athena. Orang Yunani Kuno percaya bahwa guru dari Phidias adalah Hegias dan Hageladas. Phidias adalah sahabat dari Perikles. Ketika Perikles berkuasa di Athena, Phidias ditunjuk untuk mengatur seni, arsitektur dan patung Athena. Musuh-musuh Perikles menggunakan saksi palsu yang bernama Menon untuk melawan Phidias. Akibatnya Phidias pun dipenjara dan meninggal di dalam kurungan. Hasil karya Phidias yang berada di Parthenon yaitu Athena Parthenos tersebut mengandung Golden Ratio.





    Plato (bahasa Yunani: Πλάτων) (lahir sekitar 427 SM - meninggal sekitar 347 SM) adalah seorang filusuf dan matematikawan Yunani, penulis Philosophical dialogues dan pendiri dari Akademik Platonik di Athena, sekolah tinggi ringkat pertama di dunia barat. Plato adalah murid Socrates. Pemikiran Plato pun banyak dipengaruhi oleh Socrates. Plato adalah guru dari Aristoteles. Karyanya yang paling terkenal adalah Republik (dalam bahasa Yunani Πολιτεία atau Politeia, "negeri") yang didalamnya berisi uraian garis besar pandangannya pada keadaan “ideal”. Dia juga menulis “Hukum” dan banyak dialog dimana Socrates sebagai peserta utama. Hubungan Plato dengan Golden Ratio adalah dalam karyanya yaitu “Timaeus” menyebutkan lima bangunan bentuk umum (tetrahedron, kubus, octahedron, dodecahedron, dan ikosahedron ) . Bangunan-bangunan tersebut mengandung Golden Ratio.



Euclid  ( / ju ː k l ɪ d / ; Yunani Kuno : Εὐκλείδης Eukleidēs) dikenal sebagai Euclid dari Alexandria adalah seorang matematikawan Yunani. Euclid sering disebut sebagai “Bapak Geometri”. Euclid aktif di Alexsandria pada masa pemerintahan Ptolemeus I (323-283 SM). Elements adalah salah satu karyanya yang paling berpengaruh dalam sejarah matematika. Dibukunya tersebut Euclid menyimpulkan prinsip-prinsip yang sekarang dikenal sebagai “Geometri Euclidean” dari satu set aksioma kecil. Euclid juga menulis karya-karya pada prespektif, irisan kerucut, geometri bola, nomor teori dan kekakuan. Didalam karyanya yaitu Elements, Euclid juga membuat definisi tentang Golden Ratio. Diawali pada saat Euclid melihat pentagon sama sisi dan persegi panjang, dimana keduanya dapat dipecah menjadi bagian-bagian yang lebih kecil dengan property rasio yang sama. Dalam buku yang ia tulis berjudul “Element” yang didalamnya terdapat definisi ”extreme and mean ratio”.  Euclid membuat definisi dasar yaitu:
“ Hanya terdapat satu garis yang parallel terhadap garis lainnya melalui sebuah titik ”
Golden ratio adalah istilah matematika untuk kondisi dimana jumlah kedua angka dibagi angka A sama dengan angka A dibagi angka B, dimana A>B.  Menggunakan persamaan matematika, golden ratio dapat digambarkan melalui persamaan berikut:

Namun Euclid belum menyebutkan mengenai penamaan Golden Ratio. Definisi yang diberikan oleh Euclid mendasari para ilmuwan berikutnya untuk mengembangkan Golden Ratio. Pada masa Euclid penyebutan Golden Ratio adalah ”extreme and mean ratio”.

  • Digg
  • Del.icio.us
  • StumbleUpon
  • Reddit
  • RSS
Read User's Comments0
Diposting oleh the beautiful proportion

Penamaan Golden Ratio

17.27 |

Pada awalnya Golden Ratio disebut dengan "extreme and mean ratio" sesuai dengan definisi Euclid pada abad sebelum masehi. Setelah itu, Golden ratio kembali muncul pada karya hasil eksplorasi Luca Pacioli. Pada bukunya yang berjudul "Da Divina Proportione" yang terbit pada tahun 1509, Pacioli menulis tentang Golden Ratio sebagai rasio pembagi yang paling proporsional.


    Fra Luca Bartolomeo de Pacioli adalah matematikawan dan biarawan Fransiskan asal Italia. Luca Pacioli lahir pada tahun 1445 di Sansepolcro (Tuscany) di mana ia menerima pendidikan abbaco. Ini adalah pendidikan yang difokuskan pada pengetahuan yang diperlukan untuk pedagang pada masa itu. Pacioli pindah ke Venesia sekitar 1464 , di mana ia melanjutkan pendidikannya sendiri dan bekerja sebagai guru untuk anak-anak pedagang. selama periode ini bahwa ia menulis buku pertamanya , sebuah buku aritmatika untuk murid-muridnya. Antara tahun 1472-1475 , ia menjadi seorang biarawan Fransiskan.

         Pada tahun 1475, ia mulai mengajar di Perugia. Dia terus bekerja sebagai guru privat matematika dan kemudian diperintahkan untuk berhenti mengajar di Sansepolcro pada tahun 1491. Pada tahun 1494, buku pertamanya yang akan dicetak, Summa de Arithmetica, Geometria, proportioni et proportionalità, diterbitkan di Venice. Pada 1497, ia menerima undangan dari Duke Ludovico Sforza untuk bekerja di Milan. Di sana ia bertemu, bekerja sama dengan, tinggal bersama, dan mengajarkan matematika kepada Leonardo da Vinci. 

      Pada 1499, Pacioli dan Leonardo terpaksa mengungsi ke Milan ketika Louis XII dari Perancis merebut kota dan mengusir mereka. Jalan mereka dipisahkan sekitar tahun 1506. Pacioli meninggal sekitar usia 70 pada tahun 1517, di Sansepolcro di mana ia berpikir bahwa ia telah menghabiskan sebagian besar tahun-tahun terakhirnya. 

      Pada bukunya yang berjudul De divina proportione (ditulis di Milan pada 1496-1498, yang diterbitkan di Venice pada tahun 1509), Pacioli menjelaskan tentang Golden Ratio dan penerapannya dalam bidang arsitektur.


       Lalu perkiraan rasio emas dalam bentuk pecahan desimal, yang bernilai 0,6180340.... pertama kali ditulis oleh Michael Maestlin pada tahun 1597 dalam suratnya untuk mantan muridnya Johannes Kepler.





       Michael Maestlin adalah seorang astronom dan ahli matematika Jerman, dikenal sebagai guru dari Johannes Kepler. Maestlin belajar teologi , matematika , dan astronomi di Tubinger Stift di Tübingen , sebuah kota di Württemberg . Ia lulus sebagai Master pada tahun 1571 dan melanjutkan studinya di Backnang.Pada tahun 1580 ia menjadi Profesor, pertama di University of Heidelberg , kemudian di University of Tübingen di mana ia mengajar selama 47 tahun dari 1583 . Pada tahun 1582 Maestlin menulis pengantar populer untuk astronomi .
      Kemudian perhitungan Golden Ratio dalam  bilangan desimal " sekitar 0,6180340 " ditulis pada tahun 1597 oleh Maestlin dalam sebuah surat kepada Kepler .

       Setelah itu, Golden Ratio telah berkembang. Dan ditemukan nilai lai dari Golden Ratio, yaitu berdasarkan perhitungan berikut :

Dua nilai a dan b dinyatakan berada dalam hubungan rasio emas φ jika:
\frac{a+b}{a} = \frac{a}{b} = \varphi.

      Salah satu cara untuk menemukan nilai φ adalah dengan memulai pembagian sisa. Dengan cara menyederhanakan pembilang dan penyebutnya dalam b/a = 1/φ,
\frac{a+b}{a} = 1 + \frac{b}{a} = 1 + \frac{1}{\varphi},
hal ini menunjukkan
1 + \frac{1}{\varphi} = \varphi.
Dikalikan dengan φ menghasilkan
\varphi + 1 = \varphi^2
yang dapat diatur menjadi
{\varphi}^2 - \varphi - 1 = 0.
Dengan menggunakan formula kuadrat menghasilkan jawaban positif yaitu
\varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\,39887\dots.

Penggunaan phi (φ) sebagai simbol Golden Ratio terjadi setelah Mark Barr menyarankan penggunaan huruf phi pada abad ke-20. 

 

      Mark Barr adalah seorang matematikawan Amerika yang menurut Theodore Andrea Cook, pada sekitar tahun 1909-an memberikan Golden Ratio dengan lambang phi (φ), yang merupakan inisial nama Phidias dalam huruf Yunani, Phidias merupakan pematung ternama Yunani yang hidup sekitar 450 SM.




           Pengembangan Golden Ratio masih berlangsung hingga saat ini, yang terakhir adalah yang ditemukan oleh Roger Penrose. Penrose menemukan pola baru menggunakan golden ratio untuk area pada dua ubin berbentuk rhombic (belah ketupat), dan frekuensi relatif yang terdapat pada pola. Penemuan yang dinamakan Penrose Tiling ini mendorong penemuan baru tentang kuasikristal.

  • Digg
  • Del.icio.us
  • StumbleUpon
  • Reddit
  • RSS
Read User's Comments0
Diposting oleh the beautiful proportion

Keajaibain Semesta Ditinjau Dari Golden Ratio

01.56 |

Golden Ratio– Pada Wajah Manusia

      Wajah ternyata menyimpan rasio-rasio matematika yang relatif konstan di hampir semua tipe wajah manusia. Dr Steven Markot, yang telah menghabiskan 25 tahun meneliti unsur matematika pada tubuh manusia, berhasil membuktikan di balik wajah seseorang tersembunyi rasio-rasio matematika disana. Dia meneliti 18 model wajah dari beragam suku & umur. Hasilnya? 97% memiliki pola yang sama.
 
Beberapa golden ratio pada wajah manusia adalah:

  • Panjang wajah / lebar wajah,
  • Jarak antara bibir dan titik di mana kedua alis mata bertemu / panjang hidung,
  • Panjang wajah / jarak antara ujung rahang dan titik di mana kedua alis mata bertemu,
  • Panjang mulut / lebar hidung,
  • Lebar hidung / jarak antara kedua lubang hidung,
  • Jarak antara kedua pupil / jarak antara kedua alis mata.

Golden Ratio –Pada Anatomi Tubuh Manusia

      Tubuh manusia pun tak luput dari rasio tersebut. Beberapa golden ratio pada tubuh manusia rata-rata adalah:

  • panjang dari pangkal lengan – sikut / sikut – ujung jari
  • panjang dari ubun ubun – dagu / ubun ubun –  sambungan kepala leher
  • panjang lutut ke kaki / panjang dari abdomen ke lutut…dan lain sebagainya…

Semuanya terpaku di angka 0,61… Jari-jari kita pun juga mengandung Golden Ratio.



Persegi Panjang Emas dan Rancangan pada Spiral

       Sebuah persegi panjang yang perbandingan panjang sisi-sisinya sama dengan golden ratio dikenal sebagai "persegi panjang emas." Mari kita letakkan sebuah bujur sangkar di sepanjang sisi lebar dari persegi panjang ini dan menggambar seperempat lingkaran yang menghubungkan dua sudut dari bujur sangkar ini. Kemudian, kita gambar satu bujur sangkar lagi dan seperempat lingkaran pada sisi yang selebihnya dan melakukan hal demikian pada seluruh persegi panjang yang ada pada persegi panjang utama. Jika Anda melakukan hal ini, pada akhirnya Anda akan mendapatkan sebuah spiral. 

  

      Perlu diperhatikan bahwa spiral tersebut tersusun berdasarkan golden ratio, karena panjang sisi yang dihasilkan dari masing-masing persegi tersebut membentuk barisan Fibonacci dan rasio dari barisan Fibonacci tersebut menghasilkan golden ratio.



       Spiral yang didasarkan pada golden ratio memiliki rancangan paling tak tertandingi yang dapat Anda temukan di alam. Contoh  pertama yang dapat kita berikan adalah susunan spiral pada Kerang laut. 

       Saat meneliti cangkang makhluk hidup yang digolongkan sebagai hewan bertubuh lunak atau moluska, yang hidup di dasar laut, bentuk dan struktur permukaan bagian dalam dan luar dari cangkangnya menarik perhatian para ilmuwan:



     Permukaan bagian dalamnya halus licin, sedangkan di bagian luarnya bergalur. Tubuh moluska berada di dalam cangkang, oleh karena itu permukaan bagian dalamnya haruslah halus licin. Garis pinggiran luar dari cangkang menambah kekokohan cangkang, sehingga meningkatkan kekuatannya. Bentuk-bentuk cangkang membuat orang kagum karena kesempurnaan dan sifat menguntungkan yang dihasilkan proses penciptaannya. Gagasan spiral pada cangkang terwujudkan dalam bentuk geometris sempurna, dalam bentuk rancangan yang sungguh elok dan "tajam".



     Cangkang-cangkang kebanyakan moluska tumbuh mengikuti bentuk spiral logaritmik. Sungguh tidak ada keraguan bahwa hewan-hewan ini tidak memahami perhitungan matematis paling sederhana sekalipun, apalagi bentuk spiral logaritmik. Jadi bagaimana makhluk-makhluk tersebut dapat mengetahui hal itu sebagai yang terbaik baginya untuk tumbuh? Bagaimana binatang-binatang ini, yang oleh sejumlah ilmuwan digambarkan sebagai makhluk "primitif", tahu bahwa spiral logaritmik adalah bentuk terbaik bagi mereka? Mustahil pertumbuhan semacam ini terjadi tanpa adanya suatu pengetahuan atau kecerdasan.



     Pertumbuhan mengikuti pola semacam ini digambarkan sebagai "gnomic growth" (pertumbuhan gnomis) oleh ilmuwan biologi Sir D'Arcy Thompson, seorang pakar dalam bidang tersebut, Ia menjelaskan, cangkang tersebut terus-menerus tumbuh, akan tetapi bentuknya tetap sama.



     Seseorang dapat menyaksikan salah satu contoh paling bagus dari pertumbuhan semacam ini pada seekor nautilus, yang garis tengahnya hanya beberapa sentimeter. C. Morrison menjelaskan proses pertumbuhan ini, yang sangat sulit untuk dirancang sekalipun dibantu dengan kecerdasan manusia, dengan menyatakan bahwa di sepanjang cangkang nautilus, spiral yang ada di bagian dalam memanjang dan tersusun atas sejumlah bilik yang disekat oleh dinding-dinding yang terbuat dari karang mutiara. Ketika hewan ini tumbuh, ia membentuk satu bilik lagi di mulut cangkang spiral yang berukuran lebih besar daripada bilik sebelumnya, dan bergerak maju memasuki tempat yang lebih besar ini dengan menutup pintu di belakangnya menggunakan selembar sekat karang mutiara.



       Nama ilmiah dari sejumlah hewan laut lain yang memiliki spiral logaritmik dengan rasio pertumbuhan yang berbeda-beda pada cangkang mereka adalah:



Haliotis parvus, Dolium perdix, Murex, Fusus antiquus, Scalari pretiosa, Solarium trochleare.



Ammonite, binatang laut punah yang kini ditemukan hanya dalam bentuk fosil, juga memiliki cangkang yang tumbuh mengikuti bentuk spiral logaritmik.




       Pertumbuhan mengikuti bentuk spiral pada dunia hewan tidak terbatas pada cangkang-cangkang moluska. Binatang-binatang seperti antelop, kambing dan biri-biri menyelesaikan perkembangan tanduk mereka dalam bentuk spiral yang berdasarkan golden ratio.

  • Digg
  • Del.icio.us
  • StumbleUpon
  • Reddit
  • RSS
Read User's Comments0
Diposting oleh the beautiful proportion
Langganan: Postingan (Atom)